Черненко з а медіанний фільтр. Медіанний фільтр на службі розробника

Нещодавно довелося зіткнутися з необхідністю програмної фільтрації даних АЦП. Гугленіе і куріння (різної документації) привело мене до двома технологіями: Фільтр низьких частот (ФНЧ) і Медіанний фільтр. Про ФНЧ є вельми докладна стаття в співтоваристві Easyelectronics, тому далі мова піде про медіанний фільтр.

Дисклеймер (відмазка): Ця стаття по здебільшого є практично дослівним перекладом статті з сайту embeddedgurus. Однак, перекладач (я) теж використовував наведені алгоритми в роботі, знайшов їх корисними, і, можливо, представляють інтерес для цієї спільноти.

Отже, будь-який лінійний фільтр створений, щоб пропускати сигнали в заданій смузі частот, і максимально послаблювати всі інші. Подібні фільтри незамінні, якщо потрібно усунути вплив всіляких шумів. Однак, в реальному світі вбудованих систем, розробник може зіткнутися з фактом, що ці класичні фільтри практично марні проти короткочасних потужних викидів.

Цей тип шуму зазвичай виникає від будь-якого випадкового події, такого, як електростатичний розряд, спрацював поряд з приладом брелок сигналізації та інше. При цьому вхідний сигнал може прийняти явно неможливе значення. Наприклад, з АЦП надійшли дані: 385, 389, 388, 388, 912, 388, 387. Очевидно, що значення 912 тут помилкове, і має бути відкинуто. При використанні класичного фільтра, майже напевно це велике число вплине на вихідне значення дуже сильно. Очевидним рішенням тут буде застосування медіанного фільтра.

Відповідно до своєї назви, медіанний фільтр пропускає середнє значення з безлічі значень. Зазвичай розмір цієї групи непарний, щоб уникнути двозначності при виборі середнього значення. Основна ідея-є якийсь буфер з декількома значеннями, з яких вибирається медіана.

Відмінності медіани від середнього арифметичного

Припустимо, що в одній кімнаті виявилося 19 будинків і один мільярдер. Кожен кладе на стіл гроші - бідняки з кишені, а мільярдер - з валізи. За $ 5 кладе кожен бідняк, а мільярдер - $ 1 млрд (109). У сумі виходить $ 1 000 000 095. Якщо ми розділимо гроші рівними частками на 20 осіб, то отримаємо $ 50 000 004,75. Це буде середнє арифметичне значення суми готівки, яка була у всіх 20 осіб в цій кімнаті.

Медіана в цьому випадку буде дорівнює $ 5 (полусумма десятого і одинадцятого, серединних значень рангового ряду). Можна інтерпретувати це в такий спосіб. Розділивши нашу компанію на дві рівні групи по 10 чоловік, ми можемо стверджувати, що в першій групі кожен поклав на стіл не більше $ 5, у другій таки не менше $ 5. У загальному випадку можна сказати, що медіана це те, скільки приніс з собою середня людина. Навпаки, середнє арифметичне - невідповідна характеристика, так як воно значно перевищує суму готівки, що є у середньої людини.
ru.wikipedia.org/wiki/Медиана_ (статистика)

За розміром цього безлічі розділимо фільтри на два типи:
Розмірність \u003d 3
Розмірність\u003e 3

Фільтр розмірністю 3

Розмірність три - найменша з можливих. Обчислити середнє значення можливо, використавши лише кілька операцій IF. Нижче наведено код, який реалізує цей фільтр:

Uint16_t middle_of_3 (uint16_t a, uint16_t b, uint16_t c) (uint16_t middle; if ((a<= b) && (a <= c)) { middle = (b <= c) ? b: c; } else if ((b <= a) && (b <= c)) { middle = (a <= c) ? a: c; } else { middle = (a <= b) ? a: b; } return middle; }

Фільтр розмірністю\u003e 3

Для фільтра розмірністю більше трьох пропоную скористатися алгоритмом, запропонованим Філом Екстормом (Phil Ekstrom) в Листопадовому номері журналу «Embedded Systems», і переписаного з Dynamic C на стандартний З Найджелом Джонсом (Nigel Jones). Алгоритм використовує однозв'язний список, і використовує той факт, що коли масив відсортований, видалення найстарішого значення, і додавання нового не порушує сортування.

#define STOPPER 0 / * Smaller than any datum * / #define MEDIAN_FILTER_SIZE (13) uint16_t median_filter (uint16_t datum) (struct pair (struct pair * point; / * Pointers forming list linked in sorted order * / uint16_t value; / * Values to sort * /); static struct pair buffer \u003d (0); / * Buffer of nwidth pairs * / static struct pair * datpoint \u003d buffer; / * Pointer into circular buffer of data * / static struct pair small \u003d (NULL, STOPPER ); / * Chain stopper * / static struct pair big \u003d (& small, 0); / * Pointer to head (largest) of linked list. * / struct pair * successor; / * Pointer to successor of replaced data item * / struct pair * scan; / * Pointer used to scan down the sorted list * / struct pair * scanold; / * Previous value of scan * / struct pair * median; / * Pointer to median * / uint16_t i; if (datum \u003d\u003d STOPPER ) (datum \u003d STOPPER + 1; / * No stoppers allowed. * /) if ((++ datpoint - buffer)\u003e \u003d MEDIAN_FILTER_SIZE) (datpoint \u003d buffer; / * Increment and wrap data in pointer. * /) datp oint-\u003e value \u003d datum; / * Copy in new datum * / successor \u003d datpoint-\u003e point; / * Save pointer to old value "s successor * / median \u003d / * Median initially to first in chain * / scanold \u003d NULL; / * Scanold initially null. * / Scan \u003d / * Points to pointer to first (largest) datum in chain * / / * Handle chain-out of first item in chain as special case * / if (scan-\u003e point \u003d\u003d datpoint) (scan-\u003e point \u003d successor;) scanold \u003d scan; / * Save this pointer and * / scan \u003d scan-\u003e point; / * step down chain * / / * Loop through the chain, normal loop exit via break. * / for (i \u003d 0; i< MEDIAN_FILTER_SIZE; ++i) { /* Handle odd-numbered item in chain */ if (scan->point \u003d\u003d datpoint) (scan-\u003e point \u003d successor; / * Chain out the old datum. * /) if (scan-\u003e value< datum) /* If datum is larger than scanned value,*/ { datpoint->point \u003d scanold-\u003e point; / * Chain it in here. * / Scanold-\u003e point \u003d datpoint; / * Mark it chained in. * / Datum \u003d STOPPER; ); / * Step median pointer down chain after doing odd-numbered element * / median \u003d median-\u003e point; / * Step median pointer. * / If (scan \u003d\u003d & small) (break; / * Break at end of chain * /) scanold \u003d scan; / * Save this pointer and * / scan \u003d scan-\u003e point; / * Step down chain * / / * Handle even-numbered item in chain. * / If (scan-\u003e point \u003d\u003d datpoint) (scan-\u003e point \u003d successor;) if (scan-\u003e value< datum) { datpoint->point \u003d scanold-\u003e point; scanold-\u003e point \u003d datpoint; datum \u003d STOPPER; ) If (scan \u003d\u003d & small) (break;) scanold \u003d scan; scan \u003d scan-\u003e point; ) Return median-\u003e value; )
Щоб скористатися цим кодом, просто викликаємо функцію кожен раз, коли з'являється нове значення. Вона поверне медіанне з останніх MEDIAN_FILTER_SIZE вимірювань.
Цей підхід вимагає досить багато RAM, тому що доводиться зберігати і значення, і покажчики. Однак він досить швидкий (58мкс на 40МГц PIC18).

висновки

Як і більшість інших речей в світі вбудованих систем, Медіанний фільтр має свою ціну. Наприклад, він вносить затримку в одне читання при безперервно зростаючих вхідних значеннях. До того ж, цей фільтр сильно спотворює інформацію про частоту сигналу. Звичайно, якщо нам цікава тільки постійна складова, це не створює особливих проблем.

1. Технічне завдання

Гаусів шум - 'gaussian'

Початкове зображення.

Принцип фільтрації.

Медіани давно використовувалися і вивчалися в статистиці як альтернатива середнім арифметичним значенням відліків в оцінці вибіркових середніх значень. Медианой числової послідовності х 1, х 2, ..., х n при непарному n є середній за значенням член ряду, що виходить при упорядкуванні цієї послідовності по зростанню (або зменшенням). Для парних n медіану зазвичай визначають як середнє арифметичне двох середніх відліків впорядкованої послідовності.

Медіанний фільтр являє собою віконний фільтр, послідовно ковзає по масиву сигналу, і повертає на кожному кроці один з елементів, що потрапили у вікно (апертуру) фільтра. Вихідний сигнал y k змінного медіанного фільтра шириною 2n + 1 для поточного відліку k формується з вхідного часового ряду ..., x k -1, x k, x k +1, ... відповідно до формули:

y k \u003d med (x k - n, x k - n + 1, ..., x k -1, x k, x k +1, ..., x k + n-1, x k + n),

де med (x 1, ..., x m, ..., x 2n + 1) \u003d x n + 1, x m - елементи варіаційного ряду, тобто ранжирування в порядку зростання значень xm: x 1 \u003d min (x 1, x 2, ..., x 2n + 1) ≤ x (2) ≤ x (3) ≤ ... ≤ x 2n + 1 \u003d max (x 1, x 2 , ..., x 2n + 1).

Таким чином, медіанна фільтрація здійснює заміну значень відліків в центрі апертури медіанного значенням вихідних відліків усередині апертури фільтра. На практиці апертура фільтру для спрощення алгоритмів обробки даних, як правило, встановлюється з непарним числом відліків, що і буде прийматися при розгляді в подальшому без додаткових пояснень.

Імпульсні і точкові шуми

При реєстрації, обробці і обміні даними в сучасних вимірювально-обчислювальних та інформаційних системах потоки сигналів крім корисного сигналу s (tt 0) і флуктуаційних шумів q (t) містять, як правило, імпульсні потоки g (t) \u003d d (tt k) різної інтенсивності з регулярною або хаотичною структурою:

x (t) \u003d s (t-t 0) + g (t) + q (t).

Під імпульсним шумом розуміється спотворення сигналів великими імпульсними викидами довільній полярності і малої тривалості. Причиною появи імпульсних потоків можуть бути як зовнішні імпульсні електромагнітні перешкоди, так і наведення, збої і перешкоди в роботі самих систем. Сукупність статистично розподіленого шуму і потоку квазідетермінірованних імпульсів являє собою комбіновану перешкоду. Радикальний метод боротьби з комбінованою перешкодою - застосування завадостійких кодів. Однак це призводить до зниження швидкості і ускладнення систем прийому-передачі даних. Простим, але досить ефективним альтернативним методом очищення сигналів в таких умовах є двоетапний алгоритм обробки сигналів x (t), де на першому етапі проводиться усунення з потоку x (t) шумових імпульсів, а на другому - очищення сигналу частотними фільтрами від статистичних шумів. Для сигналів, перекручених дією імпульсних шумів, відсутня сувора в математичному сенсі постановка і рішення задачі фільтрації. Відомі лише евристичні алгоритми, найбільш прийнятним з яких є алгоритм медіанної фільтрації.

Припустимо, що шум q (t) являє собою статистичний процес з нульовим математичним очікуванням, корисний сигнал s (t-t 0) має невідоме тимчасове положення t 0 Î, а потік шумових імпульсів g (t) має вигляд:

g (t) \u003d e k a k g (t-t k),

де a k - амплітуда імпульсів в потоці, t k - невідоме тимчасове положення імпульсів, e k \u003d 1 з ймовірністю p k і e k \u003d 0 з ймовірністю 1-p k. Таке завдання імпульсної перешкоди відповідає потоку Бернуллі.

При застосуванні до потоку x (t) ковзної медіанної фільтрації з вікном N відліків (N - непарне) медіанний фільтр повністю усуває поодинокі імпульси, віддалені один від одного мінімум на половину апертури фільтра, і пригнічує імпульсні перешкоди, якщо кількість імпульсів в межах апертури не перевищує (N-1) / 2. В цьому випадку, при p k \u003d p для всіх імпульсів перешкоди, ймовірність придушення перешкод може бути визначена за виразом / 3i /:

R (p) \u003d p m (1-p) N- p.

На рис.1 наведені результати розрахунків імовірності придушення імпульсної перешкоди медіанного фільтром. при p<0.5 результаты статистического моделирования процесса показывают хорошее соответствие расчетным значениям. Для интенсивных импульсных шумовых потоков при p>0.5 медіанна фільтрація стає мало ефективною, тому що відбувається не придушення, а посилення і трансформація його в потік імпульсів іншої структури (з випадковою тривалістю).

Якщо ймовірність помилки не дуже велика, то медіанна фільтрація навіть з досить малою апертурою значно зменшить кількість помилок. Ефективність виключення шумових імпульсів підвищується зі збільшенням апертури фільтра, але одночасно може збільшуватися і спотворення корисного сигналу.

Перепад плюс шум.

Розглянемо фільтрацію перепадів при наявності адитивного білого шуму, т. Е. Фільтрацію послідовностей, або зображень, з

де s - детермінований сигнал, рівний 0 по одну сторону or перепаду і h - по іншу, a z - випадкові значення білого шуму. Припустимо, що випадкові значення шуму z розподілені по нормальному закону N (0, s). Для початку розглянемо одновимірну фільтрацію і будемо вважати, що перепад відбувається в точці i \u003d 1, таким чином, що для i £ 0 величина xi є N (0, s), а для i≥1 величина х i є N (h, s ).

На рис. 2 показана послідовність значень математичного очікування медіан і змінного середнього поблизу перепаду висотою h \u003d 5 при N \u003d 3. Значення змінного середнього слідують по похилій лінії, що свідчить про змазування перепаду. Поведінка математичного очікування значень медіани також свідчить про деяке змащення, хоча в набагато менше, ніж для змінного середнього.

Якщо скористатися мірою середньоквадратичної помилки (СКП), усередненої по N точок поблизу перепаду, і обчислити значення СКО в залежності від значень h, то неважко зафіксувати, що при малих значеннях h<2 СКО для скользящего среднего немного меньше, чем для медианы, но при h>3 СКО медіани значно менше, ніж СКО середнього. Цей результат показує, що змінна медіана значно краще, ніж ковзне середнє, для перепадів великої висоти. Схожі результати можна отримати і для апертури N \u003d 5, і для двовимірної фільтрації з апертурами 3x3 і 5x5. Таким чином, математичні очікування медіани для малих h близькі до математичних очікуванням для відповідних середніх, але для великих h вони асимптотично обмежені. Пояснюється це тим, що при великих h (скажімо, h\u003e 4) змінні х із середнім значенням 0 (для даного прикладу) будуть різко відділені від змінних х із середнім h.

Використана міра точності може характеризувати тільки різкість поперек перепаду і нічого не говорить про гладкості фільтрованої зображення уздовж перепаду. Ковзне усереднення дає сигнали, гладкі уздовж перепаду, тоді як при обробці за допомогою медіанного фільтром протяжні перепади виявляються злегка порізаними.

фільтрація Вінера

Інверсна фільтрація має низьку помехоустойчивостью, тому що цей метод не враховує зашумленность спостережуваного зображення. Значно менш схильний до впливу перешкод і сингулярностей, зумовлених нулями передавальної функції спотворює системи, фільтр Вінера, тому що при його синтезі поряд з видом ФРТ використовується інформація про спектральних щільності потужності та шуму.

Спектральна щільність сигналу визначається співвідношенням:

де - автокореляційна функція.

Взаємна спектральна щільність сигналу визначається співвідношенням:

, (14)

де - функція взаємної кореляції.

При побудові фільтра Вінера ставиться завдання мінімізації середньоквадратичного відхилення обробленого зображення від предмета:

де - математичне очікування. Перетворюючи ці вирази можна показати, що мінімум досягається, коли передавальна функція визначається наступним виразом:

Подальший аналіз показує, що відновлення зображення, формування якого описується виразом повинно здійснюватися з використанням наступного ОПФ відновлює перетворювача:

Якщо шуму на зображенні немає, то спектральна щільність функції шуму дорівнює 0 і вираз, яке називають фільтром Вінера, перетворюється в звичайний зворотний фільтр.

При зменшенні спектральної щільності потужності вихідного зображення передавальна функція фільтра Вінера прагне до нуля. Для зображень це характерно на верхніх частотах.

На частотах, відповідних нулях передавальної функції формує системи, передавальна функція фільтра Вінера також дорівнює нулю. Таким чином, вирішується проблема сингулярності відновлює фільтра.

ОПФ Фільтри Вінера

інверсні фільтри

Мал. 3. Приклади фільтрів

Фільтрація зображень.

Медіанна фільтрація зображень найбільш ефективна, якщо шум на зображенні має імпульсний характер і являє собою обмежений набір пікових значень на тлі нулів. В результаті застосування медіанного фільтру похилі ділянки і різкі перепади значень яскравості на зображеннях не змінюються. Це дуже корисна властивість саме для зображень, на яких контури несуть основну інформацію.

рис.4

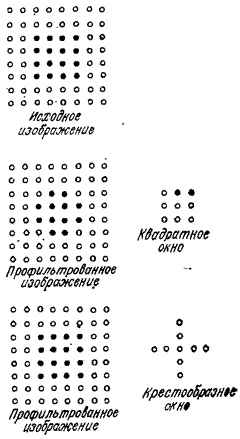
При медіанної фільтрації зашумленних зображень ступінь згладжування контурів об'єктів безпосередньо залежить від розмірів апертури фільтра та форми маски. Приклади форми масок з мінімальної апертурою наведені на малюнку 4. При малих розмірах апертури краще зберігаються контрастні деталі зображення, але в меншій мірі пригнічується імпульсні шуми. При великих розмірах апертури спостерігається зворотна картина. Оптимальний вибір форми згладжує апертури залежить від специфіки розв'язуваної задачі і форми об'єктів. Особливе значення це має для завдання збереження перепадів (різких кордонів яскравості) в зображеннях.

Під зображенням перепаду розуміємо зображення, в якому точки по одну сторону від деякої лінії мають однакове значення а, А всі крапки по іншу сторону від цієї лінії - значення b, b¹ a. Якщо апертура фільтру симетрична щодо початку координат, то медіанний фільтр зберігає будь-яке зображення перепаду. Це виконуються для всіх апертур з непарною кількістю відліків, тобто крім апертур (квадратні рамки, кільця), які не містять початку координат. Проте квадратні рамки і кільця будуть лише незначно змінювати перепад.

Для спрощення подальшого розгляду обмежимося прикладом фільтра з квадратної маскою розміром N × N, при N \u003d 3. Скользящий фільтр переглядає відліки зображення зліва-направо і зверху-вниз, при цьому вхідні двовимірну послідовність також представимо у вигляді послідовного числового ряду відліків (x (n)) зліва-направо зверху-вниз. З цієї послідовності в кожній поточній точці маска фільтра виділяє масив w (n), як W-елементний вектор, який в даному випадку містить всі елементи з вікна 3 × 3, центровані навколо x (n), і сам центральний елемент, якщо це передбачено типом маски:

w (n) \u003d.

У цьому випадку значення x i відповідає відображенню зліва-направо і зверху-вниз вікна 3 × 3 в одновимірний вектор.

Елементи даного вектора, як і для одновимірного медіанного фільтра, також можуть бути впорядковані в ряд за зростанням або спаданням своїх значень:

r (n) \u003d,

визначено значення медіани y (n) \u003d med (r (n)), і центральний відлік маски замінений значенням медіани. Якщо за типом маски центральний відлік не входить в число ряду 8, то медіанне значення знаходиться в вигляді середнього значення двох центральних відліків ряду 9.

Наведені вирази не пояснюють способу знаходження вихідного сигналу поблизу кінцевих і прикордонних точок в кінцевих послідовностях і зображеннях. Один з простих прийомів полягає в тому, що потрібно знаходити медіану тільки тих точок всередині зображення, які потрапляють в межі апертури. Тому для точок, розташованих поруч з кордонами, медіани будуть визначені, виходячи з меншого числа точок.

Медіанна фільтрація може виконуватися і в рекурсивном варіанті, при якому значення зверху і зліва від центрального відліку в масці (в даному випадку x 1 (n) -x 4 (n) на рис. 9) в ряді 8 замінюються на вже обчислені в попередніх циклах значення y 1 (n) -y 4 (n).

результати обробки

Накладення шумів на оригінальне зображення

Gaussian Salt & Paper Speckle

Результат обробки медіа фільтром

MedFilter_Gaussian MedFilter_Salt & Paper MedFilter_Speckle

Результат обробки фільтром Вінера

WinFilter_Gaussian WinFilter_ Salt & Paper WinFilter_ Speckle

Результат підрахунку среднеквадратіческогоотклоненія відфільтрованих ізображенійот оригіналу.

ВИСНОВОК

На графіку видно, що медіанний фільтр добре пригнічує поодинокі імпульсні перешкоди і випадкові шумові викиди відліків (CKOSaPeMed) і за графіком видно, що це найкращий метод щодо усунення даного виду зашумлення.

Фільтр Вінера (CKOSaPeWin), на відміну від медіанного фільтра, при збільшенні коефіцієнта зашумленности зображення, віддалявся від оригіналу в кілька разів.

Придушення білого і гаусового шуму, в разі медіанного фільтра, менш ефективно (CKOGausMed, CKOSpecMed), ніж у фільтра Вінера (CKOGausWin, CKOSpecWin). Слабка ефективність спостерігається також при фільтрації флюктуационная шуму. При збільшенні розмірів вікна медіальної фільтра відбувається розмиття зображення.

Список літератури

1. Цифрова обробка кольорових зображень. Шліхт Г.Ю. М., Видавництво ЕКОМ, 2007. - 336 с.

2. http://prodav.narod.ru/dsp/index.html

3. Введення в цифрову обробку зображень. Ярославський Л.П. М .: Сов. радіо, 2007. - 312 с.

4. http://matlab.exponenta.ru/

5. Цифрова обробка зображень в середовищі MATLAB. Р. Гонсалес, Р. Вудс, С. Еддінс, М .: Техносфера, 2006.

6. http://www.chipinfo.ru/literature/chipnews/199908/29.html

1.Технічне завдання .............................................. ......................... 2

2.Аналіз технічного завдання ............................................. ....... 3

2.1. Медіанний фільтр. Медіанна фільтрація ................... 4

2.1.1 Переваги і недоліки медіанний фільтрів .............................. 6

2.2 Принцип фільтрації ............................................... ...................... 7

2.3 Придушення статистичних шумів .................................... 8

2.4 Імпульсні і точкові шуми ............................................. ... 9

2.5 Перепад плюс шум .............................................. .......................... 11

2.6 Фільтрація Вінера ............................................... ........................ 13

2.7. Фільтрація зображень ................................................ ......... 15

2.7.1 Використання адаптивної фільтрації ..................... 17

2.7.2 Використання медіанної фільтрації ....................... 17

3. ПРОЕКТУВАННЯ ДОПОМІЖНОЇ ФУНКЦІЇ MATLAB. 18

3.1. Зчитування зображення і створення його копії ............................... 18

3.2. Додавання шумів до копії вихідного зображення ................... 18

3.3. Обробка зашумленной копії за допомогою медіанного фільтра. 18

3.4. Обробка зашумленной копії за допомогою фільтра Вінера ....... 20

3.5. Розрахунок СКО між фільтрованим зображенням і оригіналом. 21

4.Результати обробки .............................................. ...................... 23

Список літератури................................................ ............................. 26

1. Технічне завдання

Порівняння ефективності медіанного і усредняющего фільтрів

1. Створити копію вихідного зображення.

2. Додати шум до копії вихідного зображення.

Гаусів шум - 'gaussian'

Імпульсний шум - 'salt & pepper'

Мультиплікативний шум - 'speckle'

4. Одну з зашумлений копій обробити за допомогою фільтра.

5. Іншу копію обробити за допомогою фільтра 2.

7. Побудувати графіки залежності СКО відфільтрованого зображення від параметра шуму (в одних осях для різних фільтрів).

Початкове зображення.

2. Аналіз технічного завдання

Медіанні фільтри досить часто застосовуються на практиці як засіб попередньої обробки цифрових даних. Специфічною особливістю фільтрів є явно виражена вибірковість по відношенню до елементів масиву, які представляють собою немонотонну складову послідовності чисел в межах вікна (апертури) фільтра, і різко виділяються на тлі сусідніх відліків. У той же час на монотонну складову послідовності медіанний фільтр не діє, залишаючи її без змін. Завдяки цій особливості, медіанний фільтри при оптимально обраної апертурі можуть, наприклад, зберігати без спотворень різкі межі об'єктів, ефективно пригнічуючи некорельовані або слабо корельовані перешкоди і малорозмірні деталі. Ця властивість дозволяє застосовувати медіанну фільтрацію для усунення аномальних значень в масивах даних, зменшення викидів і імпульсних перешкод. Характерною особливістю медіанного фільтра є його нелінійність. У багатьох випадках застосування медіанного фільтра виявляється більш ефективним в порівнянні з лінійними фільтрами, оскільки процедури лінійної обробки є оптимальними при рівномірному або гауссова розподілі перешкод, що в реальних сигналах може бути далеко не так. У випадках, коли перепади значень сигналів великі в порівнянні з дисперсією аддитивного білого шуму, медіанний фільтр дає менше значення середньоквадратичної помилки в порівнянні з оптимальними лінійними фільтрами. Особливо ефективним медіанний фільтр виявляється при очищенні сигналів від імпульсних шумів при обробці зображень, акустичних сигналів, передачі кодових сигналів і т.п. Однак детальні дослідження властивостей медіанний фільтрів як засобу фільтрації сигналів різного типу є досить рідкісними.

Медіанний фільтр. медіанна фільтрація

В даний час методи цифрової обробки сигналів набули широкого поширення в телебаченні, радіотехніці, системах зв'язку, управління і контролю. Однією з найпоширеніших операцій при такій обробці є цифрова фільтрація сигналів.

Медіанна фільтрація була запропонована Тьюки як інструмент згладжування часових рядів, що зустрічаються в економічних дослідженнях, а в подальшому вона стала широко застосовуватися при обробці зображень, мовних сигналів і т. П.

Медіанний фільтр - один з видів цифрових фільтрів, широко використовуваний в цифровій обробці сигналів і зображень для зменшення рівня шуму. Медіанний фільтр є нелінійним КИХ-фільтром.

Значення відліків усередині вікна фільтра сортуються в порядку зростання (спадання); і значення, що знаходиться в середині упорядкованого списку, надходить на вихід фільтра. У разі парного числа відліків у вікні вихідне значення фільтра дорівнює середньому значенню двох відліків в середині упорядкованого списку. Вікно переміщається уздовж фильтруемого сигналу і обчислення повторюються.

Медіанна фільтрація - ефективна процедура обробки сигналів, що піддаються впливу імпульсних перешкод.

Медіанна фільтрація.

Медіанна фільтрація здійснює заміну значень відліків в центрі апертури медіанного значенням вихідних відліків усередині апертури фільтра. На практиці апертура фільтру для спрощення алгоритмів обробки даних, як правило, встановлюється з непарним числом відліків, що і буде прийматися при розгляді в подальшому без додаткових пояснень.

Медіанна фільтрація реалізується у вигляді процедури локальної обробки відліків в ковзному вікні, яке включає певну кількість відліків сигналу. Для кожного положення вікна виділені в ньому відліки ранжуються за зростанням або спаданням значень. Середній за своїм становищем звіт в ранжируваному списку називається медіаною даної групи відліків. Цим відліком замінюється центральний відлік у вікні для оброблюваного сигналу. В силу цього медіанний фільтр відноситься до числа нелінійних фільтрів, який заміняє медіанного значенням аномальні точки і викиди незалежно від їх амплітудних значень, і є стійким за визначенням, здатним анулювати навіть нескінченно великі відліки.

Алгоритм медіанної фільтрації має явно виражену вибірковість до елементів масиву з немонотонної складової послідовності чисел в межах апертури і найбільш ефективно виключає з сигналів поодинокі викиди, негативні і позитивні, які потрапляють на краю ранжированного списку. З урахуванням ранжирування в списку медіанний фільтри добре поглинають шуми та перешкоди, протяжність яких становить менше половини вікна. Стабільною точкою є послідовність (в одновимірному випадку) або масив (в двовимірному випадку), які не змінюються при медіанної фільтрації. В одновимірному випадку стабільними точками медіанний фільтрів є "локально-монотонні" послідовності, які медіанний фільтр залишає без змін. Виняток становлять деякі періодичні виконавчі послідовно-вательності.

Медіанна фільтрація - метод нелінійної обробки сигналів, розроблений Тьюки. Цей метод виявляється корисним при придушенні шуму на зображенні. Одновимірна медіанний фільтр являє собою ковзне вікно, яке охоплює непарне число елементів, зображення. Центральний елемент замінюється медіаною всіх елементів зображення у вікні. Медианой дискретної послідовності для непарного є той її елемент, для якого існують елементів, менших або рівних йому за величиною, і елементів, великих або рівних йому за величиною. Нехай у вікно потрапили елементи зображення з рівнями 80, 90, 200, 110 і 120; в цьому випадку центральний елемент слід замінити значенням 110, яке є медіаною впорядкованої послідовності 80, 90, 110, 120, 200. Якщо в цьому прикладі значення 200 є шумовим викидом в монотонно зростаючій послідовності, то медіанна фільтрація забезпечить істотне поліпшення. Навпаки, якщо значення 200 відповідає корисному імпульсу сигналу (при використанні широкосмугових датчиків), то обробка призведе до втрати чіткості відтвореного зображення. Таким чином, медіанний фільтр в одних випадках забезпечує придушення шуму, в інших - викликає небажане придушення сигналу.

На рис. 12.6.1 показано вплив медіанного і усереднюються (згладжує) фільтрів з пятіелементной вікном на ступінчастий, пилкоподібний, імпульсний і трикутний дискретні сигнали. З цих діаграм видно, що медіанний фільтр не впливає на ступінчасті або пилковидні функції, що зазвичай є бажаною властивістю. Однак цей фільтр пригнічує імпульсні сигнали, тривалість яких становить менше половини ширини вікна. Фільтр також викликає сплощення вершини трикутної функції.

Мал. 12.6.1. Приклади медіанної фільтрації найпростіших дискретних сигналів,.

а - ступінчастий перехід: б - пилкоподібний перехід; в - одиночний імпульс; е - здвоєний імпульс; д - строєний імпульс; е - трикутний сигнал.

Можливості аналізу дії медіанного фільтра обмежені. Можна показати, що медіана твори постійної і послідовності дорівнює

Крім того,

Однак медіана суми двох довільних послідовностей і не дорівнює сумі їх медіан:

Це нерівність можна перевірити на прикладі послідовностей 80, 90, 100, 110, 120 і 80, 90, 100, 90, 80.

Можуть бути різні стратегії застосування медіанного фільтру для придушення шумів. Одна з них рекомендує починати з медіанного фільтра, вікно якого охоплює три елементи зображення. Якщо ослаблення сигналу незначно, вікно фільтра розширюють до п'яти елементів. Так надходять до тих пір, поки медіанна фільтрація починає приносити більше шкоди, ніж користі. Інша можливість полягає в здійсненні каскадної медіанної фільтрації сигналу з використанням фіксованою або змінюваною ширини вікна. У загальному випадку ті області, які залишаються без зміни після одноразової обробки фільтром, не змінюються і після повторної обробки. Області, в яких тривалість імпульсних сигналів становить менше половини ширини вікна, будуть зазнавати змін після кожного циклу обробки.

Концепцію медіанного фільтра легко узагальнити на два виміри, застосовуючи двовимірне вікно бажаної форми, наприклад прямокутне або близьке до кругового. Очевидно, що двовимірний медіанний фільтр з вікном розміру забезпечує більш ефективне придушення шуму, ніж послідовно застосовані горизонтальний і вертикальний одномірні медіанний фільтри з вікном розміру; двовимірна обробка, однак, призводить до більш істотного послаблення сигналу. На рис. 12.6.2 показано вплив двовимірної медіанної фільтрації на просторовий імпульсний сигнал. Використовувалися фільтри з вікнами двох типів: квадратним розміру і хрестоподібним розміру. Як видно, медіанний фільтр з квадратним вікном зруйнував кути зображеного квадрата, а фільтр з хрестоподібним вікном залишив його без зміни.

Мал. 12.6.2. Приклади двовимірної медіанної фільтрації

На рис. 12.6.3 та 12.6.4 представлені зразки зображень, підданих медіанної фільтрації з метою придушення шумів. Як видно, медіанний фільтр більш ефективно пригнічує розрізнені імпульсні перешкоди, ніж гладкі шуми. Медіанну фільтрацію зображень з метою придушення шумів слід вважати евристичним методом. Її не можна застосовувати наосліп. Навпаки, слід перевіряти отримані результати, щоб переконатися в доцільності медіанної фільтрації.

Мал. 12.6.3. Зразки зображень, оброблених одновимірним медіанного фільтром з метою придушення імпульсних перешкод.

а - вихідне зображення з імпульсними перешкодами (15 перекручених елементів в кожному рядку); б - результат медіанної фільтрації при; в - результат медіанної фільтрації при; г - результат медіанної фільтрації при.

Мал. 12.6.4. Зразки зображень, оброблених одновимірним медіанного фільтром з метою придушення гауссова шуму.

а - вихідне зображення з гаусовим шумом; б - результат медіанної фільтрації при; в - результат медіанної фільтрації при; г - результат медіанної фільтрації при.

Всі лінійні алгоритми фільтрації призводять до згладжування різких перепадів яскравості зображень, що пройшли обробку. Цей недолік, особливо істотний, якщо споживачем інформації є людина, принципово не може бути виключений в рамках лінійної обробки. Справа в тому, що лінійні процедури є оптимальними при гауссовский розподілі сигналів, перешкод і спостережуваних даних. Реальні зображення, строго кажучи, не підкоряються цим розподілу ймовірностей. Причому, одна з основних причин цього полягає в наявності у зображень різноманітних кордонів, перепадів яскравості, переходів від однієї текстури до іншої і т. П. Піддаючись локальному гауссовскому опису в межах обмежених ділянок, багато реальні зображення в зв'язку з цим погано представляються як глобально гаусові об'єкти . Саме це і є причиною поганої передачі кордонів при лінійної фільтрації.

Друга особливість лінійної фільтрації - її оптимальність, як тільки що згадувалося, при гауссовский характері перешкод. Зазвичай цій умові відповідають шумові перешкоди на зображеннях, тому при їх придушенні лінійні алгоритми мають високі показники. Однак, часто доводиться мати справу з зображеннями, перекрученими перешкодами інших типів. Однією з них є імпульсна перешкода. При її впливі на зображенні спостерігаються білі або (і) чорні точки, хаотично розкидані по кадру. Застосування лінійної фільтрації в цьому випадку неефективно - кожен з вхідних імпульсів (по суті - дельта-функція) дає відгук у вигляді імпульсної характеристики фільтра, а їх сукупність сприяє поширенню перешкоди на всю площу кадру.

Вдалим рішенням перерахованих проблем є застосування медіанної фільтрації, запропонованої Дж. Тьюки в 1971 р для аналізу економічних процесів. Найбільш повне дослідження медіанної фільтрації стосовно до обробки зображень представлено в збірнику. Відзначимо, що медіанна фільтрація являє собою евристичний метод обробки, її алгоритм не є математичним рішенням строго сформульованої задачі. Тому дослідниками приділяється велика увага аналізу ефективності обробки зображень на її основі і порівнянні з іншими методами.

При застосуванні медіанного фільтра (МФ) відбувається послідовна обробка кожної точки кадру, в результаті чого утворюється послідовність оцінок. В ідейному відношенні обробка в різних точках незалежна (цим МФ схожий на масковий фільтр), але в цілях її прискорення доцільно алгоритмічно на кожному кроці використовувати раніше виконані обчислення.

При медіанної фільтрації використовується двовимірне вікно (апертура фільтру), зазвичай має центральну симетрію, при цьому його центр розташовується в поточній точці фільтрації. На рис. 3.10 показані два приклади найбільш часто вживаних варіантів вікон у вигляді хреста і у вигляді квадрата. Розміри апертури належать до числа параметрів, що оптимізуються в процесі аналізу ефективності алгоритму. Відлік зображення, що опинилися в межах вікна, утворюють робочу вибірку поточного кроку.



Мал. 3.10. Приклади вікон при медіанної фільтрації

Двовимірний характер вікна дозволяє виконувати, по суті, двовимірну фільтрацію, оскільки для утворення оцінки залучаються дані як з поточних рядки і стовпці, так і з сусідніх. Позначимо робочу вибірку у вигляді одновимірного масиву ; число його елементів дорівнює розміру вікна, а їх розташування довільно. Зазвичай застосовують вікна з непарним числом точок (це автоматично забезпечується при центральній симетрії апертури і при входженні самої центральної точки в її склад). Якщо впорядкувати послідовність по зростанню, то її медианой буде той елемент вибірки, який займає центральне положення в цій впорядкованої послідовності. Отримане таким чином число і є продуктом фільтрації для поточної точки кадру. Зрозуміло, що результат такої обробки справді не залежить від того, в якій послідовності представлені елементи зображення в робочій вибірці. Введемо формальне позначення описаної процедури у вигляді:

. (3.48)

Розглянемо приклад. Припустимо, що вибірка має вигляд:, а елемент 250, розташований в її центрі, відповідає поточній точці фільтрації (рис. 3.10). Велике значення яскравості в цій точці кадру може бути результатом впливу імпульсної (точкової) перешкоди. Упорядкована по зростанню вибірка має при цьому вид (45,55,75,99,104,110,136,158,250), отже, відповідно до процедури (3.48), отримуємо. Бачимо, що вплив "сусідів" на результат фільтрації в поточній точці призвело до "ігнорування" імпульсного викиду яскравості, що слід розглядати як ефект фільтрації. Якщо імпульсна перешкода не є точковою, а покриває деяку локальну область, то вона також може бути пригнічена. Це станеться, якщо розмір цієї локальної області буде менше, ніж половина розміру апертури МФ. Тому для придушення імпульсних перешкод, що вражають локальні ділянки зображення, слід збільшувати розміри апертури МФ.

З (3.48) випливає, що дія МФ полягає в "ігноруванні" екстремальних значень вхідний вибірки - як позитивних, так і негативних викидів. Такий принцип придушення перешкоди може бути застосований і для ослаблення шуму на зображенні. Однак дослідження придушення шуму за допомогою медіанної фільтрації показує, що її ефективність при вирішенні цього завдання нижче, ніж у лінійної фільтрації.

Результати експериментів, що ілюструють роботу МФ, наведені на рис. 3.11. В експериментах застосовувався МФ, що має квадратну апертуру зі

стороною рівною 3. У лівому ряду представлені зображення, спотворені перешкодою, в правому - результати їх медіанної фільтрації. На рис. 3.11.а і рис. 3.11.в показано вихідне зображення, спотворене імпульсною завадою. При її накладення використовувався датчик випадкових чисел з рівномірним на інтервалі законом розподілу, що виробляє у всіх точках кадру незалежні випадкові числа. Інтенсивність перешкоди задавалася ймовірністю її виникнення в кожній точці. Якщо для випадкового числа, сформованого в точці, виконувалася умова, то яскравість зображення в цій точці заміщалася числом 255, відповідним максимальної яскравості (рівню білого). На рис. 3.11.а дією імпульсної перешкоди спотворено 5% (\u003d 0.05), а на рис. 3.11.в - 10% елементів зображення. Результати обробки говорять про практично повну придушенні перешкоди в першому випадку і про її значне послаблення в другому.







Мал. 3.11. Приклади медіанної фільтрації

Мал. 3.11.д показує зображення, спотворене незалежним гауссовским шумом при відношенні сигнал / шум дБ, а рис. 3.11.е - результат його фільтрації медіанного фільтром. Умови даного експерименту дозволяють порівнювати його результати з результатами розглянутої вище лінійної фільтрації. У таблиці 3.1 наведені дані, що дають можливість такого порівняння. Для різних методів фільтрації в цій таблиці наводяться значення відносного середнього квадрата помилок і коефіцієнта ослаблення шуму для випадку, коли відношення сигнал / шум на вході фільтра становить -5 дБ.

Табл.3.1. Порівняння ефективності придушення шуму при фільтрації зображень, дБ

масковий фільтр з оптимальним. КИХ	масковий фільтр з рівномірний. КИХ	двовимірний рекурентності. фільтр	двовимірний фільтр Вінера	медіанний фільтр

Найбільшою ефективністю володіє двовимірний фільтр Вінера, що зменшує середній квадрат помилок в 17 разів. Медіанний фільтр має найменшу з усіх розглянутих фільтрів ефективність, йому відповідає \u003d 5.86. Тим не менш, це число свідчить про те, що і при його допомоги вдається значно знизити рівень шуму на зображенні.

Разом з тим, як говорилося вище, і що демонструє рис. 3.11.е, медіанна фільтрація в меншій мірі згладжує кордону зображення, ніж будь-яка лінійна фільтрація. Механізм цього явища дуже простий і полягає в наступному. Припустимо, що апертура фільтру знаходиться поблизу кордону, що розділяє світлий і темний ділянки зображення, при цьому її центр розташовується в області темного ділянки. Тоді, найімовірніше, робоча вибірка буде містити більшу кількість елементів з малими значеннями яскравості, і, отже, медіана перебуватиме серед тих елементів робочої вибірки, які відповідають цій області зображення. Ситуація змінюється на протилежну, якщо центр апертури зміщений в область більш високої яскравості. Але це і означає наявність чутливості у МФ до перепадів яскравості.

1.doc

ЦИФРОВИЙ ОБРОБКА СИГНАЛІВ

Тема 16. медіанний фільтр

Кому невідомо повсякчасне невідповідність між тим, що людина шукає, і що знаходить?

Ніколло Макіавеллі. Італійський політик, історик. 1469-1527 р

Коли маєш справу з орієнтуванням на середину - будь подвійно обережний. Соціалізм теж претендував на середній рай для всіх, а на виході отримав убогу казарму.

Ернст труби. Уральський геофізик. ХХ ст.

Вступ.

1. Медианная фільтрація одновимірних сигналів. Принцип фільтрації. Одномірні фільтри. Придушення статистичних шумів. Імпульсні і точкові шуми. Перепад плюс шум. Коваріаційні функції. Перетворення статистики шумів. Частотні характеристики фільтра. Різновиди медіанний фільтрів. Переваги медіанний фільтрів. Недоліки медіанний фільтрів.

2. Медианная фільтрація зображень. Шуми в зображеннях. Двовимірні фільтри. Адаптивні двовимірні фільтри. Фільтри на основі рангової статистики.

ВСТУП

^ 16.1. Медіанної фільтрації одновимірних сигналів.

Принцип фільтрації. Медіани давно використовувалися і вивчалися в статистиці як альтернатива середнім арифметичним значенням відліків в оцінці вибіркових середніх значень. Медианой числової послідовності х 1, х 2, ..., х n при непарному n є середній за значенням член ряду, що виходить при упорядкуванні цієї послідовності по зростанню (або зменшенням). Для парних n медіану зазвичай визначають як середнє арифметичне двох середніх відліків впорядкованої послідовності.

Медіанний фільтр являє собою віконний фільтр, послідовно ковзає по масиву сигналу, і повертає на кожному кроці один з елементів, що потрапили у вікно (апертуру) фільтра. Вихідний сигнал y k змінного медіанного фільтра шириною 2n 1 для поточного відліку k формується з вхідного часового ряду ..., x k -1, x k, x k 1, ... відповідно до формули:

Y k \u003d med (x k - n, x k - n 1, ..., x k -1, x k, x k 1, ..., x k n -1, x k n), (16.1.1)

Де med (x 1, ..., x m, ..., x 2n 1) \u003d x n 1, x m - елементи варіаційного ряду, тобто ранжирування в порядку зростання значень xm: x 1 \u003d min (x 1, x 2, ..., x 2n 1) ≤ x (2) ≤ x (3) ≤ ... ≤ x 2n 1 \u003d max (x 1, x 2, ... , x 2n 1).

Одномірні фільтри. Медіанна фільтрація реалізується у вигляді процедури локальної обробки відліків в ковзному вікні, яке включає певну кількість відліків сигналу. Для кожного положення вікна виділені в ньому відліки ранжуються за зростанням або спаданням значень. Середній за своїм становищем звіт в ранжируваному списку називається медіаною даної групи відліків. Цим відліком замінюється центральний відлік у вікні для оброблюваного сигналу. В силу цього медіанний фільтр відноситься до числа нелінійних фільтрів, який заміняє медіанного значенням аномальні точки і викиди незалежно від їх амплітудних значень, і є стійким за визначенням, здатним анулювати навіть нескінченно великі відліки.

Мал. 16.1.1.
Завдяки цій особливості, медіанний фільтри при оптимально обраної апертурі можуть зберігати без спотворень різкі межі об'єктів, пригнічуючи некорельовані і слабо корельовані перешкоди і малорозмірні деталі. За аналогічних умов алгоритми лінійної фільтрації неминуче «змазує» різкі кордону і контури об'єктів. На рис. 16.1.1 наведено приклад обробки сигналу з імпульсними шумами медіанного і трикутним фільтрами з однаковими розмірами вікна N \u003d 3. Перевага медіанного фільтра очевидно.

В якості вихідних і кінцевих умов фільтрації зазвичай приймаються кінцеві значення сигналів, або медіана знаходиться тільки для тих точок, які вписуються в межі апертури.

Мал. 16.1.2.
На рис. 16.1.2 наведено приклад медіанної фільтрації модельного сигналу a k, складеного з детермінованого сигналу s k в сумі з випадковим сигналом q k, що має рівномірний розподіл з поодинокими імпульсними викидами. Вікно фільтра дорівнює 5. Результат фільтрації - відліки b k.

Придушення статистичних шумів Медіа фільтрами в зв'язку з їх нелинейностью зазвичай розглядається тільки на якісному рівні. Не можна також чітко розмежувати вплив медіанний фільтрів на сигнал і шум.

Якщо значення елементів послідовності чисел (x i) в апертурі фільтра є незалежними однаково розподіленими (НІР) випадковими величинами із середнім значенням m

Те математичне сподівання M (z) \u003d 0 і, отже, M (x) \u003d m.

Нехай F (x) і f (x) \u003d F "(x) позначають функції розподілу і щільності ймовірностей величин х. Відповідно до теорії ймовірностей, розподіл у \u003d med (х 1, ..., х n) для великих n є приблизно нормальним N (mt,  n), де mt - теоретична медіана, яка визначається з умови F (mt) \u003d 0.5, при цьому дисперсія розподілу:

 n 2 \u003d 1 / (n 4f 2 (m t)). (16.1.2)

Наведені результати справедливі як для одновимірної, так і для двовимірної фільтрації, якщо n вибирати рівним числу точок в апертурі фільтра. Якщо f (x) симетрична щодо m, то розподіл медіан також буде симетрично щодо m і, таким чином, справедлива формула:

M (med (х 1, ..., х n)) \u003d M (x i) \u003d m.

Якщо випадкові величини х є НОР і рівномірно розподілені на відрізку, то можна знайти точне значення дисперсії медіани за формулою:

 n 2 \u003d 1 / (4 (n 2)) \u003d 3 x / (n 2).

Якщо випадкові величини х є незалежними, однаково розподіленими з нормальним розподілом N (m, ), то m t \u003d m. Модифікована формула дисперсії медіани для малих непарних значень n:

 g    2 / (2n-2 ). (16.1.2 ")

Значення дисперсії шумів для випадкових величин в ковзному n-вікні арифметичного усереднення (фільтр МНК першого порядку) має значення  2 / n. Це означає, що для нормального білого шуму при рівних значеннях n вікон медіанного фільтра і фільтра ковзаючого усереднення, дисперсія шумів на виході медіанного фільтра приблизно на 57% більше, ніж у фільтра змінного середнього. Щоб медіанний фільтр давав ту ж дисперсію, що і ковзне усереднення, його апертура повинна бути на 57% більше. При цьому слід мати на увазі, що спотворення корисних сигналів, особливо при наявності в них стрибків і крутих перепадів, навіть при більшій апертурі медіанного фільтра може виявитися менше, ніж у фільтрів змінного середнього.

Положення змінюється, якщо щільність розподілу випадкових величин істотно відрізняється від нормального і має довгі хвости, які і ліквідуються медіанного фільтром, що забезпечує оптимальну і найбільш правдоподібну оцінку поточних значень сигналу по мінімуму середньоквадратичного наближення. Так, при експоненційному (по модулю) розподілі щільності шумів

F (x) \u003d (/  exp (- | x-m | / )

Дисперсія шумів після медіанного фільтра на 50% менше, ніж після фільтра змінного середнього.

Граничним випадком таких розподілів є імпульсний шум, випадковий по амплітудам і місця появи, який і пригнічується медіа фільтрами з найбільшою ефективністю.

Імпульсні і точкові шуми . При реєстрації, обробці і обміні даними в сучасних вимірювально-обчислювальних та інформаційних системах потоки сигналів крім корисного сигналу s (t- 0) і флуктуаційних шумів q (t) містять, як правило, імпульсні потоки g (t) \u003d  (t-  k) різної інтенсивності з регулярною або хаотичною структурою

X (t) \u003d s (t- 0) g (t) q (t). (16.1.3)

Припустимо, що шум q (t) являє собою статистичний процес з нульовим математичним очікуванням, корисний сигнал s (t- 0) має невідоме тимчасове положення  0 , а потік шумових імпульсів g (t) має вигляд:

G (t) \u003d  k a k g (t- k), (16.1.4)

Де a k - амплітуда імпульсів в потоці,  k - невідоме тимчасове положення імпульсів,  k \u003d 1 з ймовірністю p k і  k \u003d 0 з ймовірністю 1-p k. Таке завдання імпульсної перешкоди відповідає потоку Бернуллі / 44 /.

R (p) \u003d p m (1-p) N - p. (16.1.5)

Мал. 16.1.3.
На рис. 16.1.3 наведені результати розрахунків імовірності придушення імпульсної перешкоди медіанного фільтром. при p<0.5 результаты статистического моделирования процесса показывают хорошее соответствие расчетным значениям. Для интенсивных импульсных шумовых потоков при p>0.5 медіанна фільтрація стає мало ефективною, тому що відбувається не придушення, а посилення і трансформація його в потік імпульсів іншої структури (з випадковою тривалістю).

Перепад плюс шум. Розглянемо фільтрацію перепадів при наявності адитивного білого шуму, т. Е. Фільтрацію послідовностей, або зображень, з

Мал. 16.1.4.
де s - детермінований сигнал, рівний 0 по одну сторону or перепаду і h - по іншу, a z - випадкові значення білого шуму. Припустимо, що випадкові значення шуму z розподілені по нормальному закону N (0, ). Для початку розглянемо одновимірну фільтрацію і будемо вважати, що перепад відбувається в точці i \u003d 1, таким чином, що для i0 величина xi є N (0, ), а для i≥1 величина х i є N (h,  ).

На рис. 16.1.4 показана послідовність значень математичного очікування медіан і змінного середнього поблизу перепаду висотою h \u003d 5 при N \u003d 3. Значення змінного середнього слідують по похилій лінії, що свідчить про змазування перепаду. Поведінка математичного очікування значень медіани також свідчить про деяке змащення, хоча в набагато менше, ніж для змінного середнього.

коваріаційні функції при білому шумі на вході. Нормалізовані функції автокореляції вихідних сигналів медіанний і усереднюються фільтрів подібні один одному. Подібність функцій кореляції пояснюється відносно високою кореляцією між медіаною і середнім, яка досягає 0.8 при великих N.

Наближена формула функції автоковаріаціі для послідовності, підданої медіанної фільтрації визначається виразом:

K () \u003d  2 / (N ( / 2) -1)) (1 | j | / N) arcsin ( (j )). (16.1.6)

Змінна медіана майже не згладжує процеси, що ведуть себе на великих інтервалах, як функції виду x i \u003d (-1) i y. Ковзне усереднення має великий згладжує дію на подібний процес, так як регулярні флуктуації значень х повністю знищуються. В цілому можна очікувати, що наближені формули коваріаційних функцій ковзають медіан будуть корисні тільки для послідовностей, на які медіанний фільтри діють так само, як і ковзне усереднення. У випадку з сильно осцилюючими послідовностями і послідовностями перепадів великої користі від них чекати не слід.

Перетворення статистики шумів. Медіанна фільтрація є нелінійної операцією над вхідним процесом, яка поряд з виключенням імпульсних перешкод змінює і розподіл статистичних шумів q (t), що може бути небажаним для побудови наступних фільтрів. Аналітичний розрахунок перетворення статистики шумів скрутний через слабку розробленість відповідного математичного апарату.

Мал. 16.1.5. Гістограми шумових сигналів.
На рис. 16.1.5 наведено приклади медіанної фільтрації модельних шумових сигналів з гаусовим і рівномірним розподілом при різній ширині вікна фільтра. Як випливає з цих графіків, при фільтрації відбувається переважне придушення шумових сигналів з великими відхиленнями відліків від середнього значення зі зменшенням стандарту (СКО - середнє відхилення) розподілу. Зменшення стандарту тим більше, чим більше вікно фільтра. Цим же визначається і перетворення форми розподілу вихідного рівномірного шуму (а також і інших розподілів шумів) до гауссових в міру збільшення розміру вікна фільтра.

Мал. 16.1.6.
На рис. 16.1.6 наведено приклад зміни гістограм шуму при виконанні дво- і трикратної послідовної фільтрації. Як видно з графіків, основний ефект фільтрації досягається на першому циклі.

Зменшення кількості великих шумових відхилень від середнього значення шуму призводить також до зміни спектра шуму і до певного придушення його високочастотних складових, яких більше в "хвостах" шумових розподілів. Це можна бачити на рис. 16.1.7 на спектрах щільності потужності вхідного і вихідного сигналів.

Мал. 16.1.7.
Нелінійність медіанної фільтрації (заміна великих відхилень середніми за рангом у вікні) призводить до підвищення низькочастотних складових спектра шуму. Цей ефект наочно видно на рис. 16.1.8, де наводяться згладжені значення відносини модулів спектрів вихідного модельного шумового сигналу до вхідного, тобто еквівалент коефіцієнта передачі фільтром шумових сигналів. На коефіцієнт передачі фільтром корисних низькочастотних сигналів це не відбивається, він залишається рівним 1, але може приводити до погіршення ставлення сигнал / шум.

Мал. 16.1.8.
Медіанний фільтр можна застосовувати і по прямо протилежного призначенням - виявлення в сигналах і виділенню квазідетермінірованних перешкод.

Частотні характеристики фільтра . Для опису лінійних фільтрів використовують імпульсну реакцію на одиничний імпульс, на ступінчасту функцію, і частотні передавальні функції в головному частотному діапазоні. Так як медіанний фільтр ліквідує поодинокі імпульси і зберігає перепади, то можна говорити, що імпульсна реакція фільтру дорівнює нулю, а відгук на ступінчасту функцію дорівнює 1. Що стосується частотної характеристики фільтра, то, в силу нелінійності фільтру, її не можна уявити будь-якої детермінованою функцією апертури і частоти. В якійсь мірі можна говорити про реакцію фільтра на косинусоидальной функції, яка також суттєво різниться для низьких і високих частот головного частотного діапазону і фази гармонік в апертурі фільтра, що можна бачити на рис. 16.1.9.

Мал. 16.1.9.
На малюнку приведено моделювання однотональний гармонік з випадковою початковою фазою. Математичні моделі сигналів задавалися в головному діапазоні спектральної області (0-2колічество точок дискретизації спектра - 2000). Модуль гармоніки встановлювався рівним 1, при цьому модуль спектра вихідного сигналу після фільтрації, по-суті, відображає передавальну функцію фільтра. Вікно медіанного фільтра дорівнює 3.

Як показує моделювання, для низьких частот, коли період гармоніки багато більше вікна апертури фільтрів, змінна медіана і ковзне середнє мають подібні характеристики, коефіцієнт передачі К п однотональний сигналів дорівнює 1. У міру зростання частоти гармоніки і в залежності від фази сигналу в апертурі фільтра починається спотворення сигналу на екстремальних значеннях (заниження екстремальних значень), і значення До п починає зменшуватися. Коли значення діафрагми медіанного фільтра стає таким же періодом сигналу, в спектрі вихідного сигналу з'являються "помилкові" гармоніки, викликані інтерференцією частоти вхідного сигналу з частотою його дискретизації (нижні графіки на малюнку 16.1.9).

Мал. 16.1.10. Медіанна фільтрація многотональная сигналів

Для многотональная вхідних сигналів починається також інтерференція частот гармонік між собою, що призводить до появи численних помилкових високочастотних гармонік (верхні графіки на рис. 16.1.10), а при наявності у вхідному сигналі високочастотних гармонік спотворюються також і коефіцієнти передачі низькочастотних гармонік (нижні графіки на малюнку), тобто частотні відгуки для одиночних гармонійних функцій не відповідають передавальним характеристикам для довільних сигналів, що є сумою косинусоидальной функцій, тому що передавальні функції стають різко нерегулярними в силу інтерференції різних частот.

Картина частотної інтерференції залежить також від фази гармонік, що підсилює нерегулярність кінцевих результатів і наочно видно на рис. 16.1.11 при різних випадкових реалізаціях фази гармонік. При збільшенні розмірів апертури фільтрів нерегулярність передачі фільтрів збільшується.

Мал. 16.1.11.
Різновиди медіанний фільтрів.

Виважено-медіанний фільтри застосовують, якщо бажано надати більшої ваги центральним точкам. Це досягається шляхом повторення k i раз кожного набору відліків в апертурі фільтра. Так, наприклад, при N \u003d 3 і k -1 \u003d k 1 \u003d 2, k 0 \u003d 3 обчислення зваженої медіани вхідного числового ряду здійснюється за формулою:

Y i \u003d med (x i - 1, x i - 1, x 0, x 0, x 0, x 1, x 1).

Така розтягнута послідовність також зберігає перепади сигналу і в певних умовах дозволяє збільшити придушення дисперсії статистичних шумів в сигналі. Жоден з вагових коефіцієнтів k i не повинен бути значно більше всіх інших.

Ітераційні медіанний фільтри виконуються послідовним повторенням медіанної фільтрації. Якщо апертура одиничної медіанної фільтрації зберігає перепади в сигналі, то вони зберігаються при итеративном застосуванні фільтра аж до тих пір, поки не припиняться зміни в фільтровану сигналі, при цьому кінцевий результат істотно відрізняється від итеративного застосування змінного середнього, де в межі виходить постійна числова послідовність. При використанні ітераційних фільтрів можна змінювати апертуру фільтра при кожному кроці ітерації.

Переваги медіанний фільтрів.

Проста структура фільтра, як для апаратної, так і для програмної реалізації.
Фільтр не змінює ступінчасті і пилковидні функції.
Фільтр добре пригнічує поодинокі імпульсні перешкоди і випадкові шумові викиди відліків.

Недоліки медіанний фільтрів.

Медіанна фільтрація нелінійна, так як медіана суми двох довільних послідовностей не дорівнює сумі їх медіан, що в ряді випадків може ускладнювати математичний аналіз сигналів.
Фільтр викликає сплощення вершин трикутних функцій.
Придушення білого і гаусового шуму менш ефективно, ніж у лінійних фільтрів. Слабка ефективність спостерігається також при фільтрації флюктуационная шуму.
При збільшенні розмірів вікна фільтра відбувається розмиття крутих змін сигналу і стрибків.

Недоліки методу можна зменшити, якщо застосовувати медіанну фільтрацію з адаптивним зміною розміру вікна фільтра в залежності від динаміки сигналу і характеру шумів (адаптивна медіанна фільтрація). Як критерій розміру вікна можна використовувати, наприклад, величину відхилення значень сусідніх відліків щодо центрального ранжированного відліку / 1i /. При зменшенні цієї величини нижче певного порогу розмір вікна збільшується.

^ 16.2. Медіанної фільтрації зображень.

Шуми в зображеннях. Ніяка система реєстрації не забезпечує ідеальної якості зображень досліджуваних об'єктів. Зображення в процесі формування їх системами (фотографічними, голографічними, телевізійними) зазвичай піддаються впливу різних випадкових перешкод або шумів. Фундаментальною проблемою в області обробки зображень є ефективне видалення шуму при збереженні важливих для подальшого розпізнавання деталей зображення. Складність вирішення даного завдання істотно залежить від характеру шумів. На відміну від детермінованих спотворень, які описуються функціональними перетвореннями вихідного зображення, для опису випадкових впливів використовують моделі адитивної, імпульсного і мультиплікативного шумів.

Найбільш поширеним видом перешкод є випадковий адитивний шум, статистично незалежний від сигналу. Модель адитивного шуму використовується тоді, коли сигнал на виході системи або на будь-якому етапі перетворення може розглядатися як сума корисного сигналу і деякого випадкового сигналу. Модель адитивного шуму добре описує дію зернистості фотоплівки, флуктуаційний шум в радіотехнічних системах, шум квантування в аналого-цифрових перетворювачів і т.п.

Адитивний гаусів шум характеризується додаванням до кожного пікселя зображення значень з нормальним розподілом і з нульовим середнім значенням. Такий шум зазвичай з'являється на етапі формування цифрових зображень. Основну інформацію в зображеннях несуть контури об'єктів. Класичні лінійні фільтри здатні ефективно видалити статистичний шум, але ступінь розмитості дрібних деталей на зображенні може перевищити допустимі значення. Для вирішення цієї проблеми використовуються нелінійні методи, наприклад алгоритми на основі анізотропної дифузії Перона і Маліка, білатеральні і трілатеральние фільтри. Суть таких методів полягає у використанні локальних оцінок, адекватних визначенням контуру на зображенні, і згладжування таких ділянок в найменшій мірі.

Імпульсний шум характеризується заміною частини пікселів на зображенні значеннями фіксованою або випадкової величини. На зображенні такі перешкоди виглядають ізольованими контрастними точками. Імпульсний шум характерний для пристроїв введення зображень з телевізійної камери, систем передачі зображень по радіоканалах, а також для цифрових систем передачі і зберігання зображень. Для видалення імпульсного шуму використовується спеціальний клас нелінійних фільтрів, побудованих на основі рангової статистики. Загальною ідеєю таких фільтрів є детектування позиції імпульсу і заміна його оцінним значенням, при збереженні інших пікселів зображення незмінними.

Двовимірні фільтри. Медіанна фільтрація зображень найбільш ефективна, якщо шум на зображенні має імпульсний характер і являє собою обмежений набір пікових значень на тлі нулів. В результаті застосування медіанного фільтру похилі ділянки і різкі перепади значень яскравості на зображеннях не змінюються. Це дуже корисна властивість саме для зображень, на яких контури несуть основну інформацію.

Мал. 16.2.1.
При медіанної фільтрації зашумленних зображень ступінь згладжування контурів об'єктів безпосередньо залежить від розмірів апертури фільтра та форми маски. Приклади форми масок з мінімальної апертурою наведені на рис. 16.2.1. При малих розмірах апертури краще зберігаються контрастні деталі зображення, але в меншій мірі пригнічується імпульсні шуми. При великих розмірах апертури спостерігається зворотна картина. Оптимальний вибір форми згладжує апертури залежить від специфіки розв'язуваної задачі і форми об'єктів. Особливе значення це має для завдання збереження перепадів (різких кордонів яскравості) в зображеннях.

Під зображенням перепаду розуміємо зображення, в якому точки по одну сторону від деякої лінії мають однакове значення а, А всі крапки по іншу сторону від цієї лінії - значення b, b a. Якщо апертура фільтру симетрична щодо початку координат, то медіанний фільтр зберігає будь-яке зображення перепаду. Це виконуються для всіх апертур з непарною кількістю відліків, тобто крім апертур (квадратні рамки, кільця), які не містять початку координат. Проте квадратні рамки і кільця будуть лише незначно змінювати перепад.

Мал. 16.2.2.
Для спрощення подальшого розгляду обмежимося прикладом фільтра з квадратної маскою розміром N × N, при N \u003d 3. Скользящий фільтр переглядає відліки зображення зліва-направо і зверху-вниз, при цьому вхідні двовимірну послідовність також представимо у вигляді послідовного числового ряду відліків (x (n)) зліва-направо зверху-вниз. З цієї послідовності в кожній поточній точці маска фільтра виділяє масив w (n), як W-елементний вектор, який в даному випадку містить всі елементи з вікна 3 × 3, центровані навколо x (n), і сам центральний елемент, якщо це передбачено типом маски:

W (n) \u003d. (16.2.1)

У цьому випадку значення x i відповідає відображенню зліва-направо і зверху-вниз вікна 3 × 3 в одновимірний вектор, як показано на рис. 16.2.2.

R (n) \u003d, (16.2.2)

Визначено значення медіани y (n) \u003d med (r (n)), і центральний відлік маски замінений значенням медіани. Якщо за типом маски центральний відлік не входить в число ряду 16.2.1, то медіанне значення знаходиться в вигляді середнього значення двох центральних відліків ряду 16.2.2.

На рис. 16.2.3 наведено приклад очищення зашумленного зображення медіанного фільтром Черненко / 2i /. Зашумлення зображення по площі становила 15%, для очищення фільтр застосований послідовно 3 рази.

Мал. 16.2.3.
Медіанна фільтрація може виконуватися і в рекурсивном варіанті, при якому значення зверху і зліва від центрального відліку в масці (в даному випадку x 1 (n) -x 4 (n) на рис. 16.2.2) в ряді 16.2.1 замінюються на вже обчислені в попередніх циклах значення y 1 (n) -y 4 (n).

Адаптивні двовимірні фільтри. Протиріччя по залежності ступеня придушення шумів і спотворення сигналу від апертури фільтра в деякій мірі згладжується при застосуванні фільтрів з динамічним розміром маски, з адаптацією розмірів апертури під характер зображення. В адаптивних фільтрах великі апертури використовуються в монотонних областях оброблюваного сигналу (краще придушення шумів), а малі - поблизу неоднорідностей, зберігаючи їх особливості, при цьому розмір ковзаючого вікна фільтра встановлюється в залежності від розподілу яскравості пікселів в масці фільтра. В їх основі лежить, як правило, аналіз яскравості околиць центральної точки маски фільтра.

Найпростіші алгоритми динамічного зміни апертури фільтра, симетричного по обох осях, зазвичай працюють за заданим на підставі емпіричних даних пороговому коефіцієнту яскравості S поріг \u003d. У кожному своє поточне місце перебування маски на зображенні ітераційний процес починається з апертури мінімального розміру. Величини відхилення яскравості сусідніх пікселів A (r, n), що потрапили у вікно розміром (n x n), відносно яскравості центрального відліку A (r) обчислюються за формулою:

S n (r) \u003d | A (r, n) / A (r) - 1 |. (16.2.3)

Критерій, за яким проводиться збільшення розміру маски з центральним відліком r і виконується наступна ітерація, має вигляд:

Max< S порог. (16.2.4)

Максимальний розмір маски (кількість ітерацій), як правило, обмежується. Для неквадратних масок, що мають розміри (n x m), ітерації можуть обчислюватися з роздільним збільшенням параметрів n і m, а також зі зміною форми масок в процесі ітерацій.

Фільтри на основі рангової статистики . В останні два десятиліття в цифровій обробці зображень активно розвиваються нелінійні алгоритми на основі рангової статистики для відновлення зображень, пошкоджених різними моделями шумів. Подібні алгоритми дозволяють уникнути додаткового спотворення зображення при видаленні шуму, а також значно поліпшити результати роботи фільтрів на зображеннях з високим ступенем зашумленности.

Сутність рангової статистики зазвичай полягає в тому, що ряд 16.2.1 не включає центральний відлік маски фільтра, і по ряду 16.2.2 проводиться обчислення значення m (n). При N \u003d 3 по рис. 16.2.2:

M (n) \u003d (x 4 (n) x 5 (n)) / 2. (16.2.5)

Обчислення вихідного значення фільтра, яким замінюється центральний відлік, виконується за формулою:

Y (n) \u003d  x (n) (1-) m (n). (16.2.6)

Значення коефіцієнта довіри  зв'язується певною залежністю зі статистикою відліків у вікні фільтра (наприклад, повної дисперсією відліків, дисперсією різниць x (n) -xi (n) або m (n) -xi (n), дисперсією позитивних і негативних різниць x (n ) -xi (n) або m (n) -xi (n), і т.п.). По суті, значення коефіцієнта  має задавати ступінь пошкодження центрального відліку і, відповідно, ступінь запозичення для його виправлення значення з відліків m (n). Вибір статистичної функції і характер залежності від неї коефіцієнта  може бути досить різноманітним і залежить як від розмірів апертури фільтра, так і від характеру зображень і шумів.

література

44. Большаков І.А., Ракошіц В.С. Прикладна теорія випадкових потоків, М .: Сов. радіо, 1978, - 248с.

46. \u200b\u200bХуанг Т.С. та ін. Швидкі алгоритми в цифровій обробці зображень. - М .: Радио и связь, 1984. - 224 с.

47. Сойфер В.А. Комп'ютерна обробка зображень. Частина 2. Методи і алгоритми. - Соросівський освітній журнал №3, 1996..

48. Апальков І.В., хрящів В.В. Видалення шуму з зображень на основі нелінійних алгоритмів з використанням рангової статистики. - Ярославський державний університет, 2007.

1i. Яровий Н.І. Адаптивна медіанна фільтрація. - http://www.controlstyle.ru/articles/science/text/amf/

2i. Черненко С.А. Медіанний фільтр. -